三角函數是基本初等函數之一，是以角度為自變量，角度對應任意角終邊與單位圓交點坐標或其比值為因變量的函數。接下來看一下常見的三角函數的圖像和性質。

三角函數的圖像

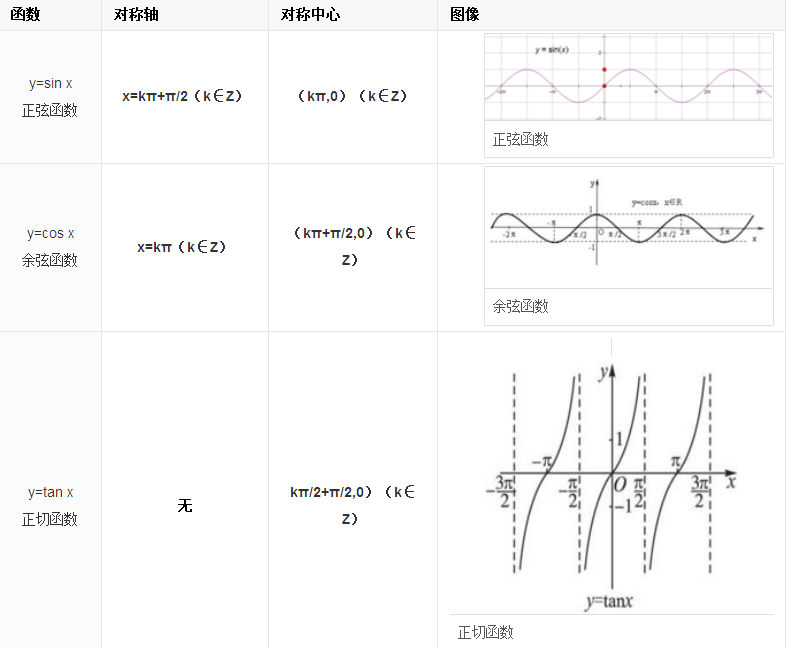
三角函數的性質

1.正弦函數

在直角三角形中，任意一銳角∠A的對邊與斜邊的比叫做∠A的正弦，記作sinA，即sinA=∠A的對邊/斜邊。

正弦值在[2kπ-π/2,2kπ+π/2](k∈Z)隨角度增大(減小)而增大(減小)，在[2kπ+π/2,2kπ+3π/2](k∈Z)隨角度增大(減小)而減小(增大)。

圖像：波形曲線

值域：[-1,1]

定義域：R

2.余弦函數

在Rt△ABC(直角三角形)中，∠C=90°(如圖所示)，∠A的余弦是它的鄰邊比三角形的斜邊，即cosA=b/c，也可寫為cosa=AC/AB。余弦函數：f(x)=cosx(x∈R)。

余弦值在[2kπ-π,2kπ](k∈Z)隨角度增大(減小)而增大(減小)，在[2kπ,2kπ+π](k∈Z)隨角度增大(減小)而減小(增大)。

圖像：波形曲線

值域：[-1,1]

定義域：R

3.正切函數

在Rt△ABC(直角三角形)中，∠C=90°，AB是∠C的對邊c，BC是∠A的對邊a，AC是∠B的對邊b，正切函數就是tanB=b/a，即tanB=AC/BC。

正切值在[kπ-π/2,kπ+π/2](k∈Z)隨角度增大(減小)而增大(減小)。

圖像：右圖平面直角坐標系反映

定義域：{x|x≠(π/2)+kπ,k∈Z}

值域：實數集R